Sebuah vektor yang diproyeksikan ke vektor lain akan menghasilkan sebuah vektor baru yang berada pada bidang vektor proyeksinya. Vektor hasil proyeksi dimungkinkan hasilnya berbeda dengan vektor semula maupun bidang vektor proyeksinya, dan juga ada kemungkinan mempunyai kesamaan dengan vektor semula maupun bidang proyeksinya.
Memproyeksikan vektor ke vektor yang lain prinsipnya hampir sama dengan menentukan jarak sebuah titik ke sebuah garis. Kenapa demikian? Ya karena dalam menentukan hasil dari sebuah vektor proyeksi, terlebih dahulu harus ditentukan jarak terdekat ujung vektor yang berupa sebuah titik ke sebuah garis yang berhimpit dengan vektor tersebut. Perhatikan gambar berikut:
Vektor u diproyeksikan ke vektor v, terlebih dahulu dicari garis yang tegak lurus terhadap vektor v dan melalui ujung vektor u. Selanjutnya, hasil dari vektor proyeksi ujungnya berada pada titik potong garis tegak lurus tersebut dengan garis yang berhimpit dengan vektor v, yaitu vektor w.
Vektor proyeksi yang dicari dari sebuah permasalahan proyeksi sebuah vektor ke vektor lain, secara geometri dapat ditampilkan menggunakan GeoGebra. Sebagai contoh kita akan menentukan hasil dari proyeksi vektor a = 3i-2j+4k pada vektor b = -i+j+2k. Langkah-langkah yang perlu dilakukan untuk menyelesaikan masalah ini adalah sebagai berikut:
1. Buka aplikasi GeoGebra dengan tampilan seperti berikut:
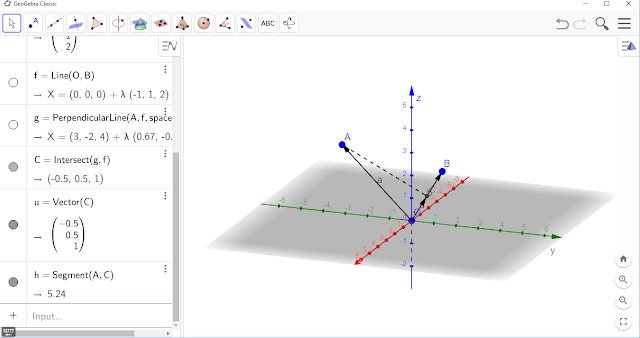
2. Buat dua vektor a dan b dengan terlebih dahulu membuat titik A= (3,-2,4) dan B= (-1,1,2), serta O=(0,0,0); gunakan perintah Vector(A) dan Vector(B)

3. Buat sebuah garis yang berhimpit pada vektor b; yaitu garis yang melalui titik O dan B

4. Gunakan tools perpendicular line, untuk menentukan sebuah garis yang tegak lurus garis OB dan melalui titik A.
5. Selanjutnya cari titik potong garis yang tegak lurus tersebut sehingga diperoleh sebuah titik (misal titik C) yang akan menjadi titik ujung dari vektor proyeksi yang dicari.
6. Buat sebuah vektor dengan perintah Vector(C)

7. Kita dapat menyembunyikan (meng- hide) garis-garis yang telah dibuat sehingga tampilan proyeksi vektor dapat dilihat seperti berikut
Terlihat bahwa vektor proyeksi a terhadap b hasilnya setengah dari vektor b, dengan hal ini dapat disimpulkan pula bahwa panjang dari vektor proyeksinya adalah setengah dari panjang vektor b.
Dengan aplikasi GeoGebra di android, kita juga dapat menyelesaikan masalah proyeksi vektor seperti halnya menggunakan GeoGebra pada laptop atau komputer. Gunakan aplikasi 3D Grapher, tutorial dapat disaksikan pada sesi akhir tulisan ini. Selamat mencoba....